Обучение математике занимает центральное место в системе начального обучения школьника, как по объёму часов, так и по значимости. От того,
каким предстанет перед учащимися математическое знание, зависит и их
отношение к обучению, и субъективный характер математического знания
младших школьников. Особую роль в начальном математическом образовании играет геометрия. Большинство специалистов в области методики обучения математике признают большие возможности геометрии в развитии учащихся.
Являясь одной из древнейших отраслей математики, геометрия обладает
значительными возможностями в формировании жизненных и ключевых
компетентностей, что, в свою очередь, повышает качество геометрического образования школьников, усиливает его положительное влияние на духовное и личностное развитие. А учитывая современную социально-экономическую ситуацию, состояние дел в развитии содержания образования, можно с уверенностью утверждать, что становление системы начального образования невозможно без развития ключевых и жизненных компетенций. Обладание ключевыми и жизненными компетенциями является одной из важнейших черт современного образования. А поэтому основывая изучение геометрии на имеющемся у учеников опыте взаимодействия с твёрдыми телами и их движением, связывая обучение с ощущениями учащихся, опираясь на естественное геометрическое развитие младших школьников, можно сделать геометрическое знание для ребёнка « живым», человеческим, имеющим самое непосредственное отношение к его повседневной жизни, а обучение геометрии более осмысленным и успешным.
Научить ребёнка смотреть на мир с геометрических позиций можно только на основе выявления и преобразования уже имеющегося у него субъектного опыта. Геометрические фигуры можно рассматривать в качестве моделей реальных объектов окружающего мира, предметные, операциональные, эмоциональные и коммуникативные представления о которых имеются в субъектном опыте ребёнка. В то же время различные реальные предметы (как уже существующие в окружающей обстановке, так и полученные в результате некоторых действий) можно рассматривать в качестве моделей геометрических объектов, причём в опыте ребёнка имеются представления о разных моделях, предусматривающих различные практические действия с ними, – изображение на бумаге, вырезанные из бумаги и твёрдых овощей, перегибание бумаги, оклеивание бумагой, натягивание шнуров, обматывание нитками, вылепливание из пластилина, составление композиций, конструирование и т.д.
Задачей учителя является создание условий для расширения и обогащения
субъективного опыта, связанного с предметами, являющимися моделями геометрических объектов, возникновения на этой основе представлений о геометрических объектах и их свойствах. Эта работа должна осуществляться в постоянном общении с учеником и требует от педагога готовности рассматривать геометрические объекты и ситуации с позиций ученика, описывать их «на языке ученика»,подбирать учебные задания для ученика и изменять их, исходя из его возможностей.
Разделом программы – «Геометрические фигуры и их свойства. Геометрические тела» предусмотрено ознакомление учащихся с фигурой:
многоугольником (четырехугольником, в том числе прямоугольником (квадратом)), его элементами – сторонами, углами, вершинами; учащиеся учатся находить периметр и площадь прямоугольника (в том числе квадрата).
Раскроем содержание работы с этими геометрическими фигурами по каждому классу отдельно.
В первом классе учащиеся знакомятся с прямоугольниками, (в том числе с четырёхугольниками). Дети должны:
– усвоить правильное название многоугольников;
– уметь их распознавать;
– определять знакомые геометрические фигуры в фигурах сложной конфигурации, на предметах окружающего мира, на рисунках;
– изображать схематично геометрические фигуры на бумаге в клеточку.
В процессе изучения нумерации чисел первого десятка практикуется составление многогранников из палочек, вырезание из бумаги, а также распознавание многоугольников на предметах окружающего мира и рисунках.
Во втором классе продолжается работа по формированию представлений
учащихся про многоугольники (в том числе прямоугольник и квадрат).
Учащиеся:
– различают геометрические фигуры;
– определяют элементы многоугольников: вершины, стороны, углы;
– обозначают геометрические фигуры буквами латинского алфавита;
– знают, что прямоугольник – это четырёхугольник, у которого все углы
прямые;
– знают, что в прямоугольнике противоположные стороны равны;
– понимают, что квадрат – это прямоугольник с одинаковыми (равными)
сторонами;
– строят прямоугольник и квадрат на бумаге в клеточку;
– знают, что периметр многоугольника – это сумма длин его сторон;
– находят периметр четырёхугольника.
Под конец обучения во 2-м классе вводятся упражнения и задания на распознавание многоугольников в конфигурациях фигур.
В третьем классе продолжается работа по формированию представлений
учащихся про периметр прямоугольника (в том числе квадрата).
Учащиеся:
– находят периметр прямоугольника (квадрата);
– решают задачи, которые связаны с периметром прямоугольника. При этом
учащимся необходимо показать разные способы вычисления периметра (а+в+а+в; а+а+в+в; а 2 + в 2; (а+в) 2;). Последний способ вычисления периметра является самым удобным (рациональным). Учащиеся должны быть ознакомлены со всеми способами, но выбирают они удобный.
В четвёртом классе – учащиеся продолжают выполнять задания на распознавание плоских и объёмных геометрических фигур и построение плоских. Знакомятся с развёрткой куба и нахождением площади поверхности куба. Решают задачи с геометрическим содержанием. Геометрические задачи, связанные с периметром, несколько усложняются, большая часть из них связана с понятием площади фигуры.
Учащиеся:
– различают плоские и объёмные геометрические фигуры;
– строят развёртку куба по образцу;
– находят общие рёбра куба, вершины для сложных граней куба;
– имеют представление о площади поверхности куба, как суммы площадей
граней.
Младшие школьники учатся распознавать эти геометрические фигуры на
моделях, рисунках и окружающих предметах. Часть геометрического содержания осознаётся детьми не на основе определений, а в результате выполнения доступных для детей практических действий. Эти геометрические фигуры используются и во время изучения других тем, что даёт возможность широко внедрять в процесс обучения комплексные упражнения: модели и изображение этих геометрических фигур используются, как дидактический материал для изучения чисел и арифметических действий над ними, для решения задач, как иллюстративный материал для формирования вычислительных навыков, для раскрытия образования частей и дробей и т.д. Программой предусмотрено овладение учащимися элементарными графическими умениями, навыками работы с чертёжными инструментами (линейкой, циркулем).
Геометрическая деятельность детей не должна связываться жесткой формально- логической схемой. И более того, геометрическая информация не должна предлагаться ученикам в готовом виде, а должна зарождаться и систематизироваться в процессе поиска, включающего в себя наблюдение, предметные действия, мысленный эксперимент. Начинать необходимо с реальных объектов и практических действий с ними, а потом учащиеся постепенно должны входить в область идеальных конструкций и абстрактных отношений.
Учитывая сказанное, знакомство младших школьников с геометрическими
объектами следует начинать с манипулирования реально существующими
предметами, которые могут рассматриваться как модели абстрактных геометрических объектов, что будет способствовать формированию их адекватных перцептивных образов. (На ранних этапах наиболее эффективными и наиболее значительно влияющими на последующее развитие зрительной ориентировки являются виды осязания, связанные с практическим манипулированием объектами.) «Рука начинает обучать глаз в процессе решения известных практических задач, связанных с захватыванием объектов и манипулированием ими ». (Запорожец А. В.).
Рассмотрим различные виды предметных действий, осваиваемых учениками начальных классов в рамках курса геометрии.
*Рисование модели на бумаге при помощи различных инструментов:
а) циркуля и линейки; б) линейки и угольника; в) линейки и сетки.
Работая в тетрадях в клетку, ученики очень рано сталкиваются с некоторыми построениями при помощи линейки и сетки. Например, в работе с младшими школьниками могут быть использованы упражнения, в которых требуется скопировать по клеткам квадрат (рис.1,а), дорисовать квадрат (рис. 2,б).
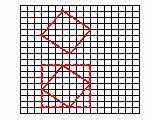
При выполнении упражнения на копирование квадрата полезно предложить учащимся проверить с помощью линейки и угольника, что данная фигура действительно является квадратом, а затем составить «маршрут» последовательного перемещения по сторонам клеток от одной вершины квадрата к другой. Этот «маршрут» можно изобразить на рисунке (например, рис.1,б) и записать с помощью слов (4 клетки вправо, 3 клетки вниз, 4 клетки вниз, 3 клетки влево и т. д.) или символов ( *4 – 3 ! * 4 ! 3 – * 4 – 3 ! * 4 ! 3 – ). Найденный «маршрут» поможет скопировать данный квадрат. Важно обратить внимание детей на повторяющиеся числа в записи «маршрута» и предложить им дорисовать квадрат (рис.2, а) с составлением соответствующего «маршрута».
Формированию у детей умения выполнять построения при помощи сетки
способствует использование геоплана – наглядного пособия, представляющего собой доску с набитой на ней гвоздевой сеткой (гвозди в узлах решетки).
Натягивая цветные резинки на гвозди, ребёнок получает модели различных
фигур.
*Получение модели из бумаги при помощи перегибания.
При помощи перегибания могут быть получены модели многих геометрических объектов. Применительно к получению модели ромба могут быть сформированы разные задачи. В частности, можно предложить детям получить ромб из листа бумаги произвольной формы и из прямоугольного листа. Например, берётся лист бумаги любой формы и перегибается один раз. Затем перегибается ещё раз так, чтобы первая и вторая линии сгибов образовали прямой угол. Отмечается на каждой линии сгиба по точке. Перегибается по линии, проходящей через эти точки. Лист бумаги разворачивается. Дети рассказывают о фигурах, которые получились при сгибании.
Из прямоугольного листа бумаги ромб может быть получен следующим
способом: прямоугольный лист бумаги нужно перегнуть по диагонали. Однослойные части получившейся фигуры отогните, накрыв ими двуслойную часть. Развернув лист бумаги, ученики рассказывают о фигурах, которые получились при сгибании (рис. 3).

*Создание модели с использованием способов построений на местности.
Построения на местности отличаются от построений на листе бумаги. Для
построений на местности используются различные инструменты. Они подробно описаны в некоторых пропедевтических курсах геометрии. Применительно к задачам, которые решаются в курсе геометрии, достаточно использовать колья и верёвки. Кольями отмечаются точки на местности, по верёвке, натянутой между кольями, проводятся прямые. В процессе обучения возможности для проведения реальных построений на местности ограничены, поэтому для освоения таких построений используются листы толстого картона, имитирующие местность, булавки, имитирующие колья, и бечёвка, имитирующая верёвку.
В качестве примера рассмотрим задачу на построение на местности прямого угла.
Прямой угол может быть построен на основе построения равнобедренного
треугольника (на середине бечёвки завязывается узел, который прокалывается булавкой, концы верёвки растягиваются и тоже прикалываются булавками, между этими двумя булавками натягивается бечёвка, находится её середина, прикалывается булавками, между ней и первой приколотой булавкой натягивается бечёвка – искомый перпендикуляр), ромба (верёвка с пятью равностоящими узлами замыкается в кольцо, первый и пятый узлы прикалываются булавкой, остальные узлы растягиваются и тоже прикалываются, пересекающиеся бечёвки, натянутые между первым и третьим, вторым и четвёртым узлами, образуют искомый прямой угол).
Подобные построения, проводимые под руководством учителя, способствуют накоплению у младших школьников эмпирического материала, формируются указания, в соответствии с которыми учащиеся могли бы выполнять такие построения.

*Получение модели с использованием шнура и трубок.
Использование таких моделей оказывает значительное влияние на расширение объёма изучаемых геометрических понятий за счёт простоты изменения формы. Эти модели изготавливаются из соломинок для коктейля, внутри которых располагается шляпная резинка. Вершины углов могут быть отмечены узлами или бусинами. Таким образом могут быть изготовлены модели многоугольников и многогранников. Работа школьников с моделью прямой призмы, основание которой – ромб с углом 60 , может быть связана с выполнением следующих учебных заданий: рассмотреть модель и найти известные фигуры; показать среди этих фигур одинаковые; рассказать, как узнали, что они одинаковые; выяснить, есть ли среди этих фигур квадраты; выяснить, может ли уместиться внутри этой призмы такой же квадрат; показать, как он будет расположен; выбрать, где на поверхности этой модели можно нарисовать самый длинный отрезок; рассказать, где он находится.
Наряду с описанными выше действиями с материальными моделями, имеющими широкую область применения, в обучении учащихся можно использовать действия с предметами, приводящие к получению моделей определённого вида. В частности, наложение друг на друга полос из цветных полупрозрачных материалов позволяет получить различные виды параллелограммов; скручивание бумажной ленты (серпантин) позволяет получить получать модели цилиндров, кругов, конусов; определённые способы перегибания квадратного листа бумаги с последующим надуванием приводит к получению модели многогранника.
А чтобы подчеркнуть специфику геометрических объектов и сделать необходимые выводы можно предложить учащимся написать своеобразное сочинение по геометрии, например: «Запишите все слова, которыми вы могли бы охарактеризовать куб, цилиндр, конус и т.д. Запишите слова, которые вам больше всего запомнились».
Такая форма деятельности благоприятна и для формирования геометрических представлений, и для развития речи детей.
Интересное решение проблемы развития устной речи учеников при изучении геометрического материала можно найти и в работе по сочинению детьми сказок о геометрических фигурах.
На уроках математики ученики могут продолжить работу над геометрическим материалом даже во время физкультминутки. Например:
«Представьте себе шар, погладьте его со всех сторон. Он большой, огромный. (Ученики «обхватывают» руками и гладят воображаемый шар.) А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до вершины. (Ученики подпрыгивают.) Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, по нижнему основанию, по боковой поверхности.
Большое значение для формирования «внутреннего, смыслового» образа геометрической фигуры имеет игра «Угадай-ка», В которую играют ученики разного возраста.
Ученики загадывают название фигуры. Один из ребят путём вопросов определяет, какая геометрическая фигура задумана. Ответами в этой игре являются слова «Да», «Нет».
- Это фигура?
- Да.
- Эта фигура плоская?
- Нет.
- У этой фигуры есть основание?
- Да.
- Эта фигура катается?
- Да.
- У этой фигуры есть вершина?
- Да.
- Эта фигура катается только по кругу?
- Это конус!
Как показывает практика, освоение учениками предметных и игровых действий, значительно расширяет возможности учителей в организации геометрической деятельности младших школьников. Знания, полученные учениками таким образом, оказываются более прочными и качественными, обеспечивается развитие пространственного мышления, математической речи школьника, а также формируется интерес к учебному предмету.